24 Appendix: tidyfault for Fault Tree Analysis

Getting Started

Fault trees are visual representation of boolean probability equations, typically depicting the sets of necessary events leading to system failure. We learned about them earlier in the textbook, but you might be wondering, with all your ggplot skills now, can you visualize a fault tree in ggplot? And are there other technical solutions for computing fault tree quantities of interest?

Good news! There is! This tutorial will explain how to use the tidyfault package to work with fault trees.

Prerequisites

As a prerequisite for this workshop, be sure to have read the Fault Trees training earlier in this book! You’ll need to install a few packages real quick below. Here they are.

install.packages(c("devtools", "admisc", "tidygraph", "ggraph", "QCA"))
# Install the tidyfault package!
devtools::install_github("timothyfraser/tidyfault")
# Select, 'install all packages'
# on the menu that will pop up in your console

Load Packages

library(dplyr)
library(readr)
library(ggplot2)
library(tidyfault)

24.1 Visualizing Fault Trees in R

We can draw fault trees easily enough by hand, but how do we record their data in a machine readable format? We can use conventions from network science to record these data in two lists: (1) an ‘edgelist’ of edges connecting nodes, and (2) a ‘nodelist’ of nodes, connected by edges.



24.1.1 Making a Nodelist

We can use the tribble() function available when loading the tidyverse package to write out small data.frames row by row. In nodes, our nodelist:

  • every node must have a unique ID, called name.

  • some events reappear multiple times in the same tree; we must give these nodes different name but the same event name.

  • each node should be classified by type as (1) an and gate, (2) an or gate, or (3) not a gate. We can use factor() to tell R to always remember "and", "or", and "not" in that order (useful for ggplot legends).

  • classic fault trees sometimes write events and the gates that condition them as separate nodes, but as far as the graph is concerned, they are really the same node. So, remember to combine them for analysis.

# Let's make a data.frame of nodes!
tribble(
  # Make the headers, using a tilde
  ~id, ~event, ~type,
  # Add the value entries
  "T",   "T",   "top",
  "G1",  "G1",  "and",
  # Notice how event 'B' appears twice,
  # so it has a logical but differentiated `name` "B1" and "B2"?
  "B1",  "B",   "not",
  "B2",  "B",   "not",
  "C1",  "C",   "not") %>%
  # Classify 'type' as a factor, with specific levels
  mutate(type = factor(type, levels = c("top", "and", "or", "not")))
## # A tibble: 5 × 3
##   id    event type 
##   <chr> <chr> <fct>
## 1 T     T     top  
## 2 G1    G1    and  
## 3 B1    B     not  
## 4 B2    B     not  
## 5 C1    C     not



24.1.2 Making an Edgelist

Next, we can use tribble() to make an edgelist of our fault tree (or use read_csv() to read in an edgelist). Edgelists should follow these conventions:

  • each row shows a unique edge between nodes, recording their node ids from the top-down in the from and to columns.
# For example....
tribble(
  ~from, ~to,
  "T",   "G1",
  "G1", "G2",
  "G2", "B1",
  "G2", "G5") 
## # A tibble: 4 × 2
##   from  to   
##   <chr> <chr>
## 1 T     G1   
## 2 G1    G2   
## 3 G2    B1   
## 4 G2    G5

24.2 Our Data

In this example, we’re going to use the default data in tidyfault, called fakenodes and fakeedges. You can download it like this:

data("fakenodes")
data("fakeedges")
fakenodes
## # A tibble: 12 × 3
##       id event type 
##    <dbl> <chr> <fct>
##  1     1 T     top  
##  2     2 G1    and  
##  3     3 G2    and  
##  4     4 G3    or   
##  5     5 G4    and  
##  6     6 G5    or   
##  7     7 A     not  
##  8     8 B     not  
##  9     9 B     not  
## 10    10 C     not  
## 11    11 C     not  
## 12    12 D     not
fakeedges
## # A tibble: 11 × 2
##     from    to
##    <dbl> <dbl>
##  1     1     2
##  2     2     3
##  3     3     8
##  4     3     6
##  5     6    10
##  6     6    12
##  7     2     4
##  8     4     7
##  9     4     5
## 10     5     9
## 11     5    11



24.3 Getting a Fault Tree Layout

Using tidyfault‘s illustrate() function, we can quickly assign x and y coordinates for a ’tree’ layout to to our fakenodes and fakeedges. We say type = "both" because we want to receive coordinates for both the nodes and edges.

gg = illustrate(nodes = fakenodes, edges = fakeedges, 
                type = "both", node_key = "id")

This returns a list() object. list() objects are collections of data.frames - sort of like a vector whose values are entire data.frames. We can query the values inside lists by using the $, just like a data.frame.

# see the nodes
gg$nodes %>% head(3)
##    x y id event type
## 1  0 4  1     T  top
## 2  0 3  2    G1  and
## 3 -1 2  3    G2  and
# see the edges
gg$edges %>% head(3)
## # A tibble: 3 × 5
## # Groups:   edge_id [2]
##   edge_id direction    id     x     y
##     <int> <chr>     <dbl> <dbl> <dbl>
## 1       1 from          1     0     4
## 2       1 to            2     0     3
## 3       2 from          2     0     3

24.4 Visualize a Fault Tree

ggplot() +
  # Plot each line corresponding to the unique edge id, used to group them
  geom_line(data = gg$edges, mapping = aes(x = x, y = y, group = edge_id)) +
  # Plot each point
  geom_point(data = gg$nodes, 
             mapping = aes(x = x, y = y, shape = type, fill = type),
             size = 10) +
  # Plot labels!
  geom_text(data = gg$nodes, mapping = aes(x = x, y = y, label = event)) +
  # We can also assign shapes!
  # (shapes 21, 22, 23, 24, and 25 have fill and color)
  scale_shape_manual(values = c(22, 24, 25, 21)) +
  # And assign some poppy colors here
  scale_fill_manual(values = c("darkgrey", "cyan", "coral", "lightgrey")) +
  # Finally, we can make a clean void theme, with the legend below.
  theme_void(base_size = 14) +
  theme(legend.position = "bottom")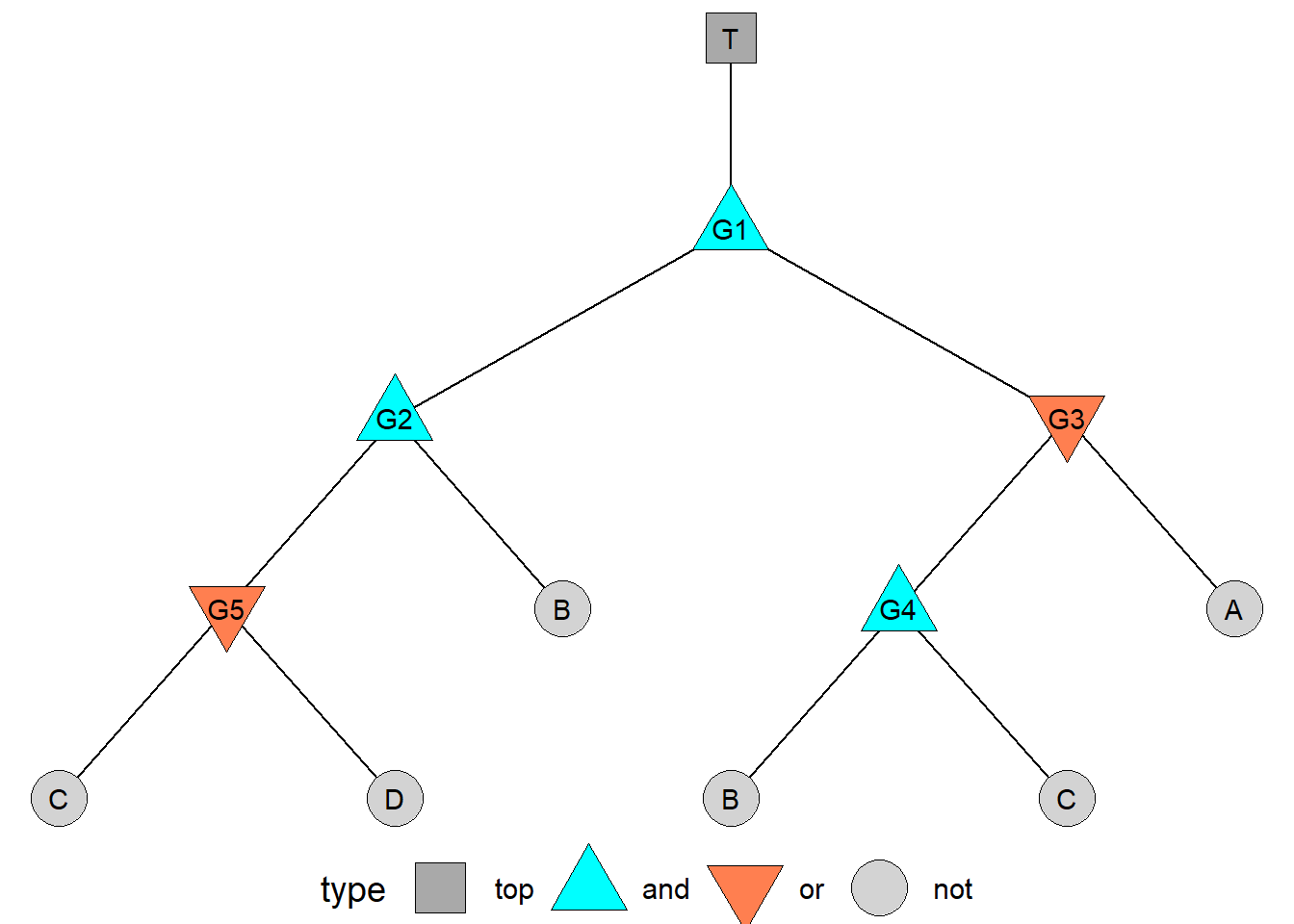



24.5 Cutsets

Fault Trees are big - and some events are more critical than others. We want to identify two kinds of information.

  1. cutsets: all the possible sets of events which together trigger failure, called cutsets.

  2. minimal cutsets: the most reduced set of events which trigger failure.

To do this, we’re going to use an algorithm, called the MOCUS top-down algorithm. I wrote it in R for you! Yay!

24.6 Gates

# To get a data.frame of gates, use curate()!
g = curate(fakenodes, fakeedges)
# Check it
g
## # A tibble: 6 × 6
##   gate  type  class     n set           items    
##   <chr> <fct> <fct> <int> <chr>         <list>   
## 1 T     top   top       1 " (G1) "      <chr [1]>
## 2 G1    and   gate      2 " (G2 * G3) " <chr [2]>
## 3 G2    and   gate      2 " (B * G5) "  <chr [2]>
## 4 G3    or    gate      2 " (A + G4) "  <chr [2]>
## 5 G4    and   gate      2 " (B * C) "   <chr [2]>
## 6 G5    or    gate      2 " (C + D) "   <chr [2]>

24.7 Equations

To get the full boolean equation of the fault tree, use equate()!

g %>% equate() 
## [1] " ( ( (B *  (C + D) )  *  (A +  (B * C) ) ) ) "

We can format it as a function too!

f = g %>% equate() %>% formulate()

# Suppose there is each of these probabilities that A, B, C, and D occur
# what's the probability of the top event?
f(A = 0.3, B = 0.5, C = 0.1, D = 0.5)
## [1] 0.105

24.8 Minimal Cutsets

To simplify down to the minimal cutsets, use concentrate()! It’s pretty quick for small graphs, but gets exponentially longer the more nodes you add. (Especially with OR statements.) That’s MOCUS’s value as well as its tradeoff.

m = g %>% 
  concentrate(method = "mocus")
# 
m
## [1] "B*C"   "A*B*D"

24.9 Coverage

We might want to know, how important are each of my minimal cutsets? We can compute the total number of cutsets that include the minimal cutset, the total cutsets leading to failure in general, and the percentage (coverage) of cutsets containing your minimal cutset out of all total cutsets leading to failure. It’s basically a measure of the explanatory power of your cutsets!

m %>% 
  tabulate(formula = f)
## # A tibble: 2 × 5
##   mincut query                                        cutsets failures coverage
##   <chr>  <chr>                                          <int>    <int>    <dbl>
## 1 A*B*D  filter(A == 1, B == 1, D == 1, outcome == 1)       2        5      0.4
## 2 B*C    filter(B == 1, C == 1, outcome == 1)               4        5      0.8

Conclusion

Happy Fault Tree analysis!