32 Appendix: Statistical Tables and Common Equations

32.1 Table 1: Chi-Squared

Table 1: Chi2 Statistics
Chi2 = qchisq(p = ci, df)
confidence interval ci = 1 - alpha level
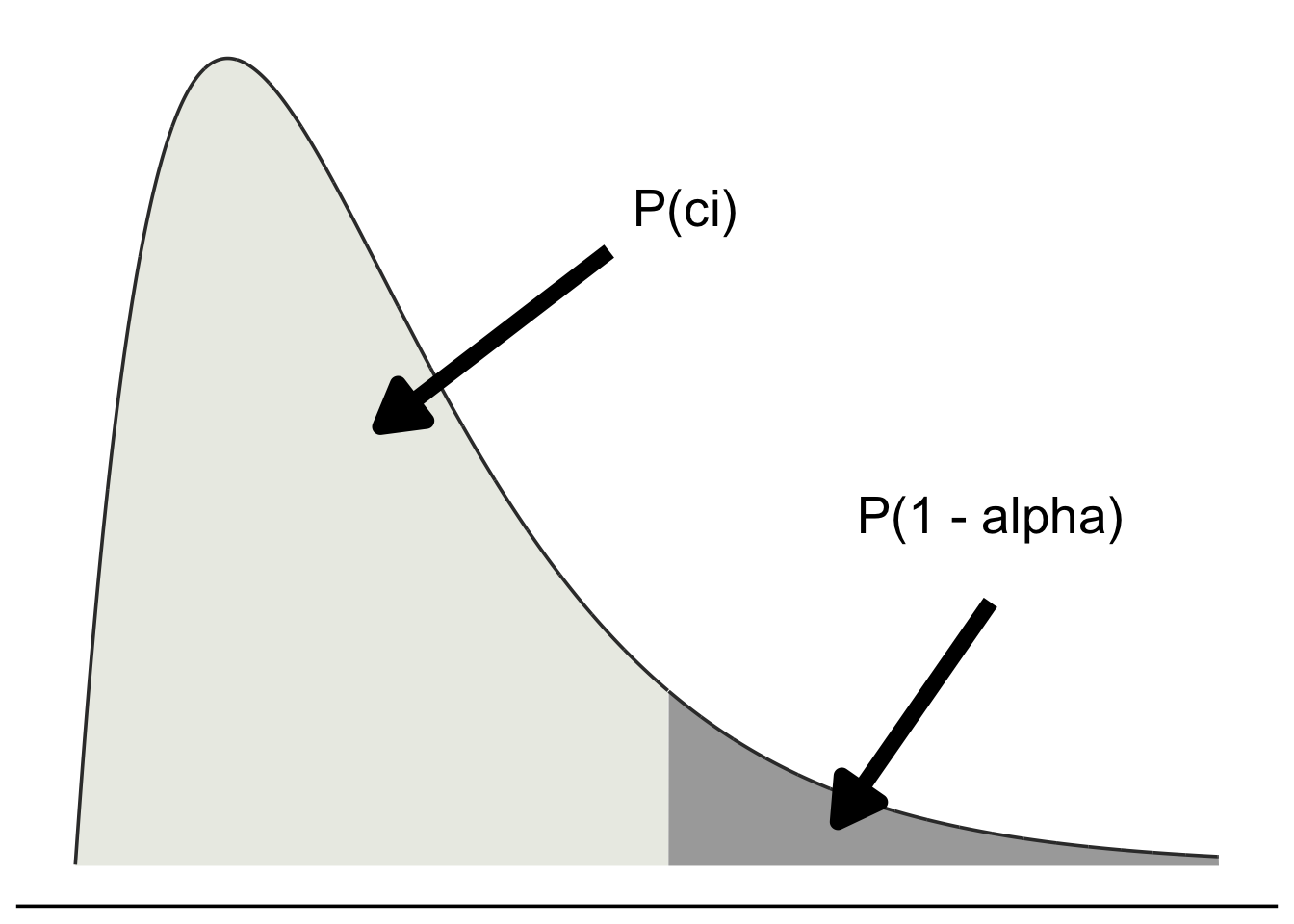
df 0.5% 2.5% 80% 90% 95% 97.5% 98% 99% 99.5% 99.8% 99.9%
1 0.0000392 0.0009820 1.64 2.70 3.84 5.02 5.41 6.63 7.87 9.54 10.82
2 0.010 0.050 3.21 4.60 5.99 7.37 7.82 9.21 10.59 12.42 13.81
3 0.071 0.215 4.64 6.25 7.81 9.34 9.83 11.34 12.83 14.79 16.26
4 0.20 0.48 5.98 7.77 9.48 11.14 11.66 13.27 14.86 16.92 18.46
5 0.41 0.83 7.28 9.23 11.07 12.83 13.38 15.08 16.74 18.90 20.51
6 0.67 1.23 8.55 10.64 12.59 14.44 15.03 16.81 18.54 20.79 22.45
7 0.98 1.68 9.80 12.01 14.06 16.01 16.62 18.47 20.27 22.60 24.32
8 1.34 2.17 11.03 13.36 15.50 17.53 18.16 20.09 21.95 24.35 26.12
9 1.73 2.70 12.24 14.68 16.91 19.02 19.67 21.66 23.58 26.05 27.87
10 2.15 3.24 13.44 15.98 18.30 20.48 21.16 23.20 25.18 27.72 29.58
11 2.60 3.81 14.63 17.27 19.67 21.92 22.61 24.72 26.75 29.35 31.26
12 3.07 4.40 15.81 18.54 21.02 23.33 24.05 26.21 28.29 30.95 32.90
13 3.56 5.00 16.98 19.81 22.36 24.73 25.47 27.68 29.81 32.53 34.52
14 4.07 5.62 18.15 21.06 23.68 26.11 26.87 29.14 31.31 34.09 36.12
15 4.60 6.26 19.31 22.30 24.99 27.48 28.25 30.57 32.80 35.62 37.69
16 5.14 6.90 20.46 23.54 26.29 28.84 29.63 31.99 34.26 37.14 39.25
17 5.69 7.56 21.61 24.76 27.58 30.19 30.99 33.40 35.71 38.64 40.79
18 6.26 8.23 22.75 25.98 28.86 31.52 32.34 34.80 37.15 40.13 42.31
19 6.84 8.90 23.90 27.20 30.14 32.85 33.68 36.19 38.58 41.61 43.82
20 7.43 9.59 25.03 28.41 31.41 34.16 35.01 37.56 39.99 43.07 45.31
21 8.03 10.28 26.17 29.61 32.67 35.47 36.34 38.93 41.40 44.52 46.79


32.2 Table 2: k-factor rules

Table 32.1: Table 2: Rules for Finding k-factors
Data Censor Bounds Rule Code Steps
Complete None both \(k_{ci,r} = \chi^{2}_{ci, 2r} \times \frac{1}{2r}\) qchisq(ci, df = 2r) / (2r) Lookup r in Table 3 or 4.
Type I Time lower \(k_{ci,r} = \chi^{2}_{ci, 2r} \times \frac{1}{2r}\) qchisq(ci, df = 2r) / (2r) Lookup r in Table 4.
Type I Time upper \(k_{ci,r} = \chi^{2}_{ci, 2(r + 1)} \times \frac{1}{2r}\) qchisq(ci, df = 2(r + 1)) / (2r) Lookup r + 1 in Table 3.
Type II Failures lower \(k_{ci,r} = \chi^{2}_{ci, 2r} \times \frac{1}{2r}\) qchisq(ci, df = 2r) / (2r) Lookup r in Table 4.
Type II Failures upper \(k_{ci,r} = \chi^{2}_{ci, 2((r-1) + 1)} \times \frac{1}{2(r - 1)} \times \frac{(r - 1)}{r}\) qchisq(ci, df = 2 * ( (r - 1) + 1)) / (2 * (r - 1) ) * (r - 1) / r Lookup r - 1 in Table 3. Multiply k by \(\frac{(r-1)}{r}\).

32.3 Table 3: k-factor (upper)

Table 3: k-factors for One-Sided Exponential Upper Bound
Time/Type I Censoring; If Type II Censoring, be sure to adjust.
k-upper = qchisq(ci, df = 2(r+1)) / (2r)
r fails
confidence interval (ci = 1 - alpha level)
r 60% 80% 90% 95% 97.5% 99% 99.9%
1 2.02 2.99 3.89 4.74 5.57 6.64 9.23
2 1.55 2.14 2.66 3.15 3.61 4.20 5.61
3 1.39 1.84 2.23 2.58 2.92 3.35 4.35
4 1.31 1.68 2.00 2.29 2.56 2.90 3.70
5 1.26 1.58 1.85 2.10 2.33 2.62 3.29
6 1.22 1.51 1.76 1.97 2.18 2.43 3.01
7 1.20 1.46 1.68 1.88 2.06 2.29 2.80
8 1.18 1.42 1.62 1.80 1.97 2.18 2.64
9 1.16 1.39 1.58 1.75 1.90 2.09 2.52
10 1.15 1.37 1.54 1.70 1.84 2.01 2.41
11 1.14 1.34 1.51 1.66 1.79 1.95 2.33
12 1.13 1.32 1.48 1.62 1.75 1.90 2.25
13 1.12 1.31 1.46 1.59 1.71 1.86 2.19
14 1.12 1.29 1.44 1.56 1.68 1.82 2.13
15 1.11 1.28 1.42 1.54 1.65 1.78 2.08
16 1.11 1.27 1.40 1.52 1.62 1.75 2.04
17 1.10 1.26 1.39 1.50 1.60 1.72 2.00
18 1.10 1.25 1.38 1.48 1.58 1.70 1.96
19 1.10 1.24 1.36 1.47 1.56 1.68 1.93
20 1.09 1.24 1.35 1.45 1.54 1.66 1.90
21 1.09 1.23 1.34 1.44 1.53 1.64 1.87
22 1.09 1.22 1.33 1.43 1.51 1.62 1.85
23 1.08 1.22 1.32 1.42 1.50 1.60 1.83
24 1.08 1.21 1.32 1.41 1.49 1.59 1.81
25 1.08 1.21 1.31 1.40 1.48 1.57 1.79
26 1.08 1.20 1.30 1.39 1.47 1.56 1.77
27 1.07 1.20 1.29 1.38 1.45 1.55 1.75
28 1.07 1.19 1.29 1.37 1.45 1.53 1.73
29 1.07 1.19 1.28 1.36 1.44 1.52 1.72
30 1.07 1.19 1.28 1.36 1.43 1.51 1.70
31 1.07 1.18 1.27 1.35 1.42 1.50 1.69
32 1.07 1.18 1.27 1.34 1.41 1.49 1.68
33 1.07 1.18 1.26 1.34 1.40 1.49 1.66
34 1.06 1.17 1.26 1.33 1.40 1.48 1.65
35 1.06 1.17 1.25 1.33 1.39 1.47 1.64
36 1.06 1.17 1.25 1.32 1.38 1.46 1.63
37 1.06 1.16 1.25 1.32 1.38 1.45 1.62
38 1.06 1.16 1.24 1.31 1.37 1.45 1.61
39 1.06 1.16 1.24 1.31 1.37 1.44 1.60
40 1.06 1.16 1.23 1.30 1.36 1.43 1.59
41 1.06 1.15 1.23 1.30 1.36 1.43 1.58


32.4 Table 4: k-factor (lower)

fix = function(x, n){x %>% format(scientific = FALSE) %>%  
    str_extract(paste(".[0-9]+[.][0-9]{", n, "}", sep = ""))}

table_k_lower = tidyr::expand_grid(
  r = c(1:41),
  alpha = c(0.60, .80, 0.90, .95, .975, .99, .999)) %>%
  mutate(
    # Calculate chi-squared for each percentile and df
    k = qchisq(1 - alpha, df = (2*r)) / (2*r)) %>%
  mutate(k = k %>% round(2)) %>%
  mutate(ci = paste((1 - alpha) * 100, "%", sep = "")) %>%
  tidyr::pivot_wider(id_cols = c(r), names_from = ci, values_from = k)

table_k_lower %>% write_csv("workshops/k_lower.csv")

k3 = table_k_lower %>%
  kable(booktabs = TRUE, format = "html", align = "c", escape = TRUE) %>%
  add_header_above(
    bold = TRUE, escape = FALSE,
    header = c("r fails" = 1, "confidence interval (ci = 1 - alpha level)"  = 7)) %>%
  add_header_above(italic = TRUE, header = c(" " = 1, "k-upper = qchisq(ci, df = 2*r) / (2*r)" = 7)) %>%
  add_header_above(bold = TRUE, header = c(" " = 1, "Type I & II Censoring, No Censoring" = 7)) %>%
  add_header_above(bold = TRUE, header = c("Table 4: k-factors for One-Sided Exponential Lower Bound" = 8)) %>%
  column_spec(1,border_right = TRUE) %>%
  kable_styling(font_size = 12, bootstrap_options = c("striped", "responsive"),full_width = TRUE) 
# View table
k3
Table 4: k-factors for One-Sided Exponential Lower Bound
Type I & II Censoring, No Censoring
k-upper = qchisq(ci, df = 2r) / (2r)
r fails
confidence interval (ci = 1 - alpha level)
r 40% 20% 10% 5% 2.5% 1% 0.1%
1 0.51 0.22 0.11 0.05 0.03 0.01 0.00
2 0.69 0.41 0.27 0.18 0.12 0.07 0.02
3 0.76 0.51 0.37 0.27 0.21 0.15 0.06
4 0.80 0.57 0.44 0.34 0.27 0.21 0.11
5 0.83 0.62 0.49 0.39 0.32 0.26 0.15
6 0.85 0.65 0.53 0.44 0.37 0.30 0.18
7 0.86 0.68 0.56 0.47 0.40 0.33 0.22
8 0.87 0.70 0.58 0.50 0.43 0.36 0.25
9 0.88 0.71 0.60 0.52 0.46 0.39 0.27
10 0.89 0.73 0.62 0.54 0.48 0.41 0.30
11 0.90 0.74 0.64 0.56 0.50 0.43 0.32
12 0.90 0.75 0.65 0.58 0.52 0.45 0.34
13 0.91 0.76 0.67 0.59 0.53 0.47 0.35
14 0.91 0.77 0.68 0.60 0.55 0.48 0.37
15 0.91 0.78 0.69 0.62 0.56 0.50 0.39
16 0.92 0.79 0.70 0.63 0.57 0.51 0.40
17 0.92 0.79 0.70 0.64 0.58 0.52 0.41
18 0.92 0.80 0.71 0.65 0.59 0.53 0.43
19 0.93 0.80 0.72 0.65 0.60 0.54 0.44
20 0.93 0.81 0.73 0.66 0.61 0.55 0.45
21 0.93 0.81 0.73 0.67 0.62 0.56 0.46
22 0.93 0.82 0.74 0.68 0.63 0.57 0.47
23 0.93 0.82 0.74 0.68 0.63 0.58 0.48
24 0.94 0.83 0.75 0.69 0.64 0.59 0.49
25 0.94 0.83 0.75 0.70 0.65 0.59 0.49
26 0.94 0.83 0.76 0.70 0.65 0.60 0.50
27 0.94 0.84 0.76 0.71 0.66 0.61 0.51
28 0.94 0.84 0.77 0.71 0.66 0.61 0.52
29 0.94 0.84 0.77 0.72 0.67 0.62 0.52
30 0.94 0.84 0.77 0.72 0.67 0.62 0.53
31 0.94 0.85 0.78 0.72 0.68 0.63 0.54
32 0.95 0.85 0.78 0.73 0.68 0.64 0.54
33 0.95 0.85 0.78 0.73 0.69 0.64 0.55
34 0.95 0.85 0.79 0.74 0.69 0.64 0.55
35 0.95 0.86 0.79 0.74 0.70 0.65 0.56
36 0.95 0.86 0.79 0.74 0.70 0.65 0.56
37 0.95 0.86 0.80 0.75 0.70 0.66 0.57
38 0.95 0.86 0.80 0.75 0.71 0.66 0.57
39 0.95 0.86 0.80 0.75 0.71 0.67 0.58
40 0.95 0.87 0.80 0.75 0.71 0.67 0.58
41 0.95 0.87 0.81 0.76 0.72 0.67 0.59


32.5 Table 5: Control Constants (d)

d-factor control constants
Subgroup Size
Control Constants
n d2 d3 D3 D4
2 1.116 0.850 0.000 3.285
3 1.691 0.890 0.000 2.579
4 2.053 0.869 0.000 2.271
5 2.328 0.869 0.000 2.120
6 2.531 0.851 0.000 2.009
7 2.712 0.837 0.074 1.926
8 2.837 0.815 0.138 1.862
9 2.979 0.819 0.175 1.825
10 3.068 0.795 0.223 1.777
11 3.190 0.792 0.256 1.744
12 3.258 0.768 0.293 1.707
13 3.340 0.771 0.308 1.692
14 3.409 0.765 0.326 1.674
15 3.475 0.757 0.346 1.654
16 3.536 0.750 0.364 1.636
17 3.584 0.739 0.381 1.619
18 3.637 0.733 0.395 1.605
19 3.667 0.726 0.406 1.594
20 3.728 0.732 0.411 1.589
21 3.777 0.716 0.431 1.569
22 3.807 0.704 0.445 1.555
23 3.853 0.714 0.444 1.556
24 3.889 0.716 0.448 1.552
25 3.933 0.714 0.455 1.545
26 3.966 0.700 0.470 1.530
27 3.987 0.697 0.475 1.525
28 4.027 0.703 0.476 1.524
29 4.051 0.690 0.489 1.511
30 4.079 0.694 0.489 1.511
31 4.109 0.690 0.496 1.504
32 4.138 0.694 0.497 1.503
33 4.155 0.678 0.511 1.489
34 4.188 0.671 0.519 1.481
35 4.211 0.675 0.519 1.481
36 4.242 0.673 0.524 1.476
37 4.260 0.669 0.529 1.471
38 4.278 0.677 0.526 1.474
39 4.301 0.678 0.527 1.473
40 4.309 0.670 0.534 1.466
41 4.346 0.674 0.535 1.465
42 4.355 0.672 0.537 1.463
43 4.374 0.660 0.547 1.453
44 4.395 0.663 0.548 1.452
45 4.418 0.657 0.554 1.446
46 4.420 0.655 0.555 1.445
47 4.453 0.663 0.554 1.446
48 4.473 0.669 0.551 1.449
49 4.491 0.650 0.566 1.434
50 4.513 0.651 0.567 1.433

32.6 Table 6: Control Constants (b)

b-factor control constants
Subgroup Size
Control Constants
n b2 b3 C4 A3 B3 B4
2 0.796 0.601 0.796 2.665 0.000 3.267
3 0.882 0.459 0.882 1.963 0.000 2.561
4 0.918 0.388 0.918 1.633 0.000 2.269
5 0.935 0.335 0.935 1.436 0.000 2.074
6 0.949 0.304 0.949 1.291 0.039 1.961
7 0.954 0.283 0.954 1.189 0.109 1.891
8 0.968 0.264 0.968 1.095 0.183 1.817
9 0.968 0.247 0.968 1.033 0.235 1.765
10 0.975 0.233 0.975 0.973 0.284 1.716
11 0.978 0.222 0.978 0.925 0.318 1.682
12 0.980 0.212 0.980 0.884 0.350 1.650
13 0.979 0.200 0.979 0.850 0.386 1.614
14 0.982 0.193 0.982 0.817 0.409 1.591
15 0.984 0.183 0.984 0.787 0.441 1.559
16 0.985 0.180 0.985 0.761 0.452 1.548
17 0.980 0.175 0.980 0.742 0.466 1.534
18 0.986 0.173 0.986 0.717 0.474 1.526
19 0.986 0.166 0.986 0.698 0.496 1.504
20 0.985 0.161 0.985 0.681 0.511 1.489
21 0.987 0.158 0.987 0.663 0.521 1.479
22 0.988 0.152 0.988 0.647 0.538 1.462
23 0.986 0.149 0.986 0.634 0.547 1.453
24 0.991 0.147 0.991 0.618 0.556 1.444
25 0.987 0.145 0.987 0.608 0.560 1.440
26 0.990 0.140 0.990 0.595 0.576 1.424
27 0.992 0.136 0.992 0.582 0.589 1.411
28 0.990 0.135 0.990 0.572 0.591 1.409
29 0.989 0.131 0.989 0.563 0.602 1.398
30 0.992 0.132 0.992 0.552 0.601 1.399
31 0.992 0.129 0.992 0.543 0.611 1.389
32 0.992 0.128 0.992 0.535 0.613 1.387
33 0.993 0.126 0.993 0.526 0.620 1.380
34 0.992 0.124 0.992 0.518 0.625 1.375
35 0.993 0.120 0.993 0.511 0.637 1.363
36 0.992 0.118 0.992 0.504 0.643 1.357
37 0.996 0.117 0.996 0.495 0.647 1.353
38 0.991 0.116 0.991 0.491 0.648 1.352
39 0.993 0.114 0.993 0.484 0.654 1.346
40 0.994 0.113 0.994 0.477 0.659 1.341
41 0.994 0.112 0.994 0.471 0.661 1.339
42 0.995 0.109 0.995 0.465 0.671 1.329
43 0.994 0.110 0.994 0.460 0.669 1.331
44 0.997 0.108 0.997 0.454 0.676 1.324
45 0.996 0.107 0.996 0.449 0.679 1.321
46 0.995 0.105 0.995 0.445 0.684 1.316
47 0.996 0.103 0.996 0.440 0.691 1.309
48 0.993 0.102 0.993 0.436 0.692 1.308
49 0.996 0.101 0.996 0.430 0.696 1.304
50 0.992 0.100 0.992 0.427 0.697 1.303

32.7 Formula

c1 = box(title = "Exponential Distribution",
    span("$$ f(t) = \\lambda e^{-\\lambda t } $$"),
    span("$$ F(t) = 1 - e^{-\\lambda t } $$"),
    span("$$ MTTF = \\frac{1}{\\lambda} $$"))

c2 = box(title = "Weibull Distribution",
    span("$$ f(t) = \\frac{m}{c} (\\frac{t}{c})^{m-1} \\times e^{-(t / c)^m } $$"),
    span("$$ F(t) = 1 - e^{-(t/c)^m} $$")
)

c3 = box(
  title = "Estimating Lambda",
  span("$$ \\hat{\\lambda} = \\frac{r}{\\sum_{i=1}^{r}{ t_i } + (n - r) \\times T_{max}  } $$"),
  span("$$ Type \\ I: \\ T_{max} = \\ end \\ of \\ study \\ period \\\\ Type \\ II: \\ T_{max} = \\ time \\ of \\ last \\ failure $$")
)

c4 = box(title = "Maximum Failure Rate",
         span("$$  \\ when \\ r \\geq 1 \\ failures \\\\ \\lambda_{(1 - \\alpha)} = \\hat{\\lambda} \\times k_{ \\ r, (1-\\alpha)} $$"),
         span("$$ when \\ r = 0 \\ failures \\\\ \\lambda_{(1 - \\alpha)} = \\frac{-ln(\\alpha ) }{n \\times T} $$"))

c5 = box(title = "Chi-squared Statistic",
         span("$$ \\chi^{2} = \\sum{ \\frac{(observed - expected)^{2} }{ expected }} $$ "),
         span("$$ Degrees \\ of \\ Freedom \\ (df) \\ for \\ \\chi^{2} \\\\ df = n_{intervals}  - 1 - n_{parameters} $$")
         )

c6 = box(title = "Process Indices",
         span("$$ C_{p} = \\frac{ E_{upper} - E_{lower} }{6 \\sigma_{short} }
              \\\\
              C_{pk} = \\frac{ | E_{limit} - \\mu | }{3 \\sigma_{short} } $$"),
         span("$$ P_{p} = \\frac{ E_{upper} - E_{lower} }{6 \\sigma_{total} }
              \\\\
              P_{pk} = \\frac{ | E_{limit} - \\mu | }{3 \\sigma_{total} } $$"),
         
         )
bslib::layout_column_wrap(
  c1, c2, c3, c4, c5, c6,
  width = 0.5,
  fill = TRUE
)
Exponential Distribution
$$ f(t) = \lambda e^{-\lambda t } $$ $$ F(t) = 1 - e^{-\lambda t } $$ $$ MTTF = \frac{1}{\lambda} $$
Weibull Distribution
$$ f(t) = \frac{m}{c} (\frac{t}{c})^{m-1} \times e^{-(t / c)^m } $$ $$ F(t) = 1 - e^{-(t/c)^m} $$
Estimating Lambda
$$ \hat{\lambda} = \frac{r}{\sum_{i=1}^{r}{ t_i } + (n - r) \times T_{max} } $$ $$ Type \ I: \ T_{max} = \ end \ of \ study \ period \\ Type \ II: \ T_{max} = \ time \ of \ last \ failure $$
Maximum Failure Rate
$$ \ when \ r \geq 1 \ failures \\ \lambda_{(1 - \alpha)} = \hat{\lambda} \times k_{ \ r, (1-\alpha)} $$ $$ when \ r = 0 \ failures \\ \lambda_{(1 - \alpha)} = \frac{-ln(\alpha ) }{n \times T} $$
Chi-squared Statistic
$$ \chi^{2} = \sum{ \frac{(observed - expected)^{2} }{ expected }} $$ $$ Degrees \ of \ Freedom \ (df) \ for \ \chi^{2} \\ df = n_{intervals} - 1 - n_{parameters} $$
Process Indices
$$ C_{p} = \frac{ E_{upper} - E_{lower} }{6 \sigma_{short} } \\ C_{pk} = \frac{ | E_{limit} - \mu | }{3 \sigma_{short} } $$ $$ P_{p} = \frac{ E_{upper} - E_{lower} }{6 \sigma_{total} } \\ P_{pk} = \frac{ | E_{limit} - \mu | }{3 \sigma_{total} } $$